dj-woo.github.io
[Paper review] TimeSformer
[Paper review] TimeSformer
title = Is Space-Time Attention All You Need for Video Understanding?
author = Gedas Bertasius and Heng Wang and Lorenzo Torresani
year = 9 Feb 2021
2020.2.9일에 나온 논문으로 Action Recognition & Action Classfication task에서 상위에 rank되어 있습니다. Video classfication에서 self-attention만을 활용한 TimeSformer를 제안하였으며, 아래와 같은 특징이 있습니다.
- conceptually simple
- state-of-the-art results on major action recognition benchmarks
- low inference cost
- suitable for long-term video modeling
1. Introduction
Natural Language Processing(NLP) 분야에서는 self-attention을 사용한 Transformer(2017)가 나오면서, revolution이 있었습니다. Transformer는 capturing long-range dependencies, training scalability에 장점이 있고, 이러한 Transformer를 사용한 다양한 방법이 NLP분야에서 나왔습니다.
Video understanding의 경우, 1.sequence data인 점, 2.문맥적 이해가 필요한 점에서 NLP와 비슷한 특징을 보이는데요. 이러한 특징을 기반으로 Transformer 기반의 long-range self-attention model이 video modeling에도 잘 작동할거라고 예상했습니다. 이를 통해, convolution operator가 내재적으로 가지고 있는 아래와 같은 제한 요소를 피할 수 있을거라 생각했습니다.
- CNN의 inductive biases (e.g., local connectivity and translation equivariance)은 small training set에서는 장점이 됩니다. 하지만, 데이터가 충분하여, 모든 걸 data에서 학습이 가능한 경우, model이 표현할 수 있는 범위를 제한할 수 있습니다. Transformer는 inductive biase가 상대적으로 적은 구조입니다.
- CNN은 short-range spatiotemporal information capture에 특화된 구조입니다. 그래서 receptive field를 벗어난 영역에 대해서는 capture가 어렵습니다. 물론, layer를 deep하게 만들어서 receptive field를 넓힐 수는 있지만, layer를 넘는 과정에서 수행되는 mean과 같은 함수가 long-range dependency capture를 어렵게 합니다. Transformer는 pair-to-pair간 직접 비교를 하기 때문에, short-range와 long-range 모두 capture할 수 있습니다.
- CNN 대비, Transformer가 GPU hardware acceleration에 더 적합한 구조를 가지고 있습니다.
그래서 기존에 video modeling에서 주를 이루던 convolution operator를 사용하지 않고 self-attention만으로 이루어진 architecture를 제안합니다.
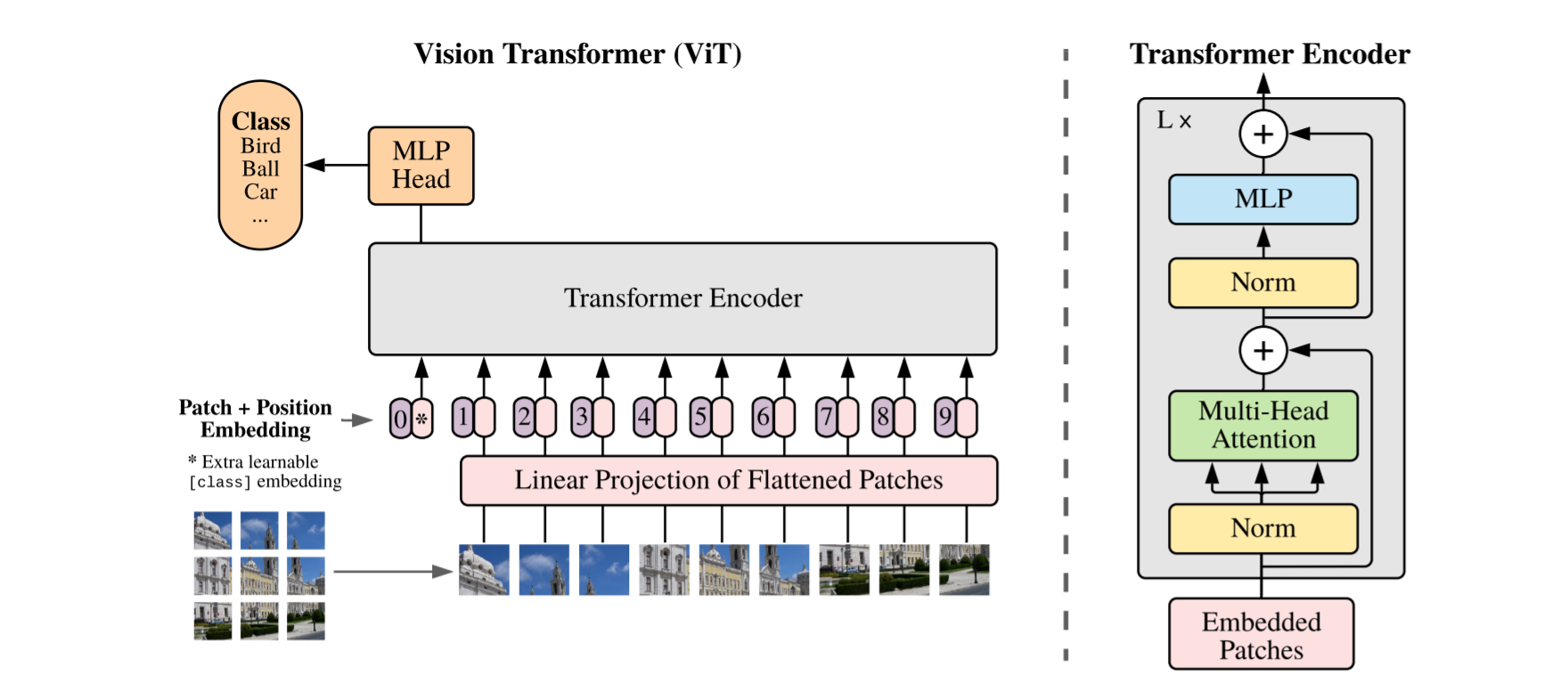
이를 위해, Vision Transformer를 확장하여, self-attention의 범위를 image space와 time space로 확장하였습니다. 제안하는 architecture인 TimeSformer(from Time-Space Transformer)는 video를 각 frame에서 뽑은 patch의 list 형태로 변환하여 처리합니다.
self-attention의 단점 중 하나가, pair-to-pari 연산을 위한 compution power인데요. 이를 극복하기 위한 방법으로, diveded attention을 사용한 방법도 같이 제안합니다.
기존에 나왔있던 방법들에 대해서 간단히 언급합니다.
- self-attention을 image classification에서 사용한 model
- image networks leveraging에 self-attention을 사용한 model들
- individual pixels를 사용한 model
- full images를 사용하기 위해, sparse key-value sampling을 이용한 model
- self-attention을 축 방향으로만 사용한 model (이 방법은 본논문에서도 일부 사용합니다.)
- Transformers를 CNN에서 나온 feature를 aggregation용으로 사용한 model들 (for action localization and recognition)
- text Transformers과 video CNNs을 같이 사용한 model들 (for various video-language tasks)
3. The TimeSformer Model
Input clip
video에서 아래와 같은 형식으로 sampiling합니다.
논문에서는 일반적으로 8x224×224x3을 사용하며, 추가적으로 high-resolution용으로 16×448×448x3를, long-range로 96×224×224x3를 사용합니다.
$$ X ∈ R^{FxH×W×3}\tag{0} $$
Decomposition into patches
ViT와 같이, 각 frame에서 non-overlapping으로 $ P \times P$ size Path $N$개를 뽑습니다.
이렇게 뽑은 patches를 vectors $x_{(p,t)} ∈ R^{3P^2}$로 flatten하게 정렬합니다.
$p = 1, . . . , N$는 하나의 frame상 spatial locations$t = 1, . . . , F$는 frame의 index
Linear embedding
path를 embedding vector로 project합니다. $$z^{(0)}_{(p,t)} = Ex_{(p,t)} + e^{pos}_{(p,t)}\tag{1} $$
- patch:
$x_{(p,t)}$ - embedding vector:
$z^{(0)}_{(p,t)} ∈ R^D$ - learnable matrix:
$E ∈ R^{D×3P^2}$ - learnable positional embedding vectore:
$e^{pos}_{(p,t)} ∈ R^D$
이때 BERT와 마찬가지로, sequence의 처음에는 classification을 위한 특별한 vecoter를 넣습니다.
Query-Key-Value computation
TimeSformer에는 L개의 encoding block이 있으며, 각 block $\ell$의 query/key/value vector는 이전 layer$\ell-1$의 output patch에서 생성됩니다.
$$q^{(\ell,a)}_{(p,t)} = W^{(\ell,a)}_Q LN \bigg( z^{(\ell−1)}_{(p,t)} \bigg) ∈ R^{D_h} \tag{2} $$ $$k^{(\ell,a)}_{(p,t)} = W^{(\ell,a)}_K LN \bigg( z^{(\ell−1)}_{(p,t)} \bigg) ∈ R^{D_h} \tag{3} $$ $$v^{(\ell,a)}_{(p,t)} = W^{(\ell,a)}_V LN \bigg( z^{(\ell−1)}_{(p,t)} \bigg) ∈ R^{D_h} \tag{4} $$
$LN()$: LayerNorm$a = 1, . . . , A$: index over multiple attention heads$A$: the total number of attention heads$D_h$=$D/A$
Self-attention computation
Self-attention weights은 dot-product로 연산됩니다. self-attention weights$α^{(\ell,a)}_{(p,t)} ∈ R^{NF+1}$는 아래와 같이 계산됩니다.
$$α^{(\ell,a)}_{(p,t)} = SM \biggl( \frac{q^{(\ell,a)}_{(p,t)}}{\sqrt{D_h}}\ \cdot\ \biggl[ k^{(\ell,a)}_{(0,0)} \bigg\{ k^{(\ell,a)}_{(p^\prime,t^\prime)} \bigg\}_{p^\prime=1,...,N\\t^\prime=1,...,F} \biggl] \biggl) \tag{5} $$
$SM()$: softmax activation function
식 (5)는 spatial-temporal 양방향 self-attention입니다. 이를 spatial-only로 제한하면, 계산량을 NxF+1에서 N+1로 줄일 수 있습니다.
Encoding
Layer $\ell$의 $z^{(\ell)}_{(p,t)}$는 아래와 같이 계산할 수 있습니다. multi-head attention layer의 output $s^{(\ell,a)}_{(p,t)}$를 계산합니다.
$$s^{(\ell,a)}_{(p,t)} = α^{(\ell,a)}_{(p,t),(0,0)} v^{(\ell,a)}_{(0,0)} +\sum_{p^\prime=1}^N \sum_{t^\prime=1}^F α^{(\ell,a)}_{(p,t),(p^\prime,t^\prime)} v^{(\ell,a)}_{(p^\prime,t^\prime)} \tag{6} $$
multi head의 output을 모두 concatation 후, projection합니다. 그후 residual connection을 추가하, LN과 MLP layer를 통과합니다. 그후 다시 residual connection을 추가합니다.
$${z^\prime}^{(\ell)}_{(p,t)} = W_O \biggl[ s^{(\ell,1)}_{(p,t)},...,s^{(\ell,A)}_{(p,t)}\biggl] +z^{(\ell-1)}_{(p,t)}\tag{7}$$ $$z^{(\ell)}_{(p,t)} = MLP(LN({z^\prime}^{(\ell)}_{(p,t)})) + {z^\prime}^{(\ell)}_{(p,t)}\tag{8} $$
이러한 encoder구조는 ViT와 동일합니다.
Classification embedding
최종 classification은 마지막 encoding layer의 첫번째 token을 사용하여 진행합니다. 이때, MLP를 한단 더 추가하여, target class와 같은 size의 vectore를 생성합니다.
Space-Time Self-Attention Models
앞에서 언급한것 처럼, spatiotempolar attention, 식(5),를 space-only 또는 time-only attention으로 변경하여 computation time을 줄일 수 있습니다. 하지만 이러한 방식은 다른 방향의 dependecy를 무시하여 accuracy를 저하시킵니다.
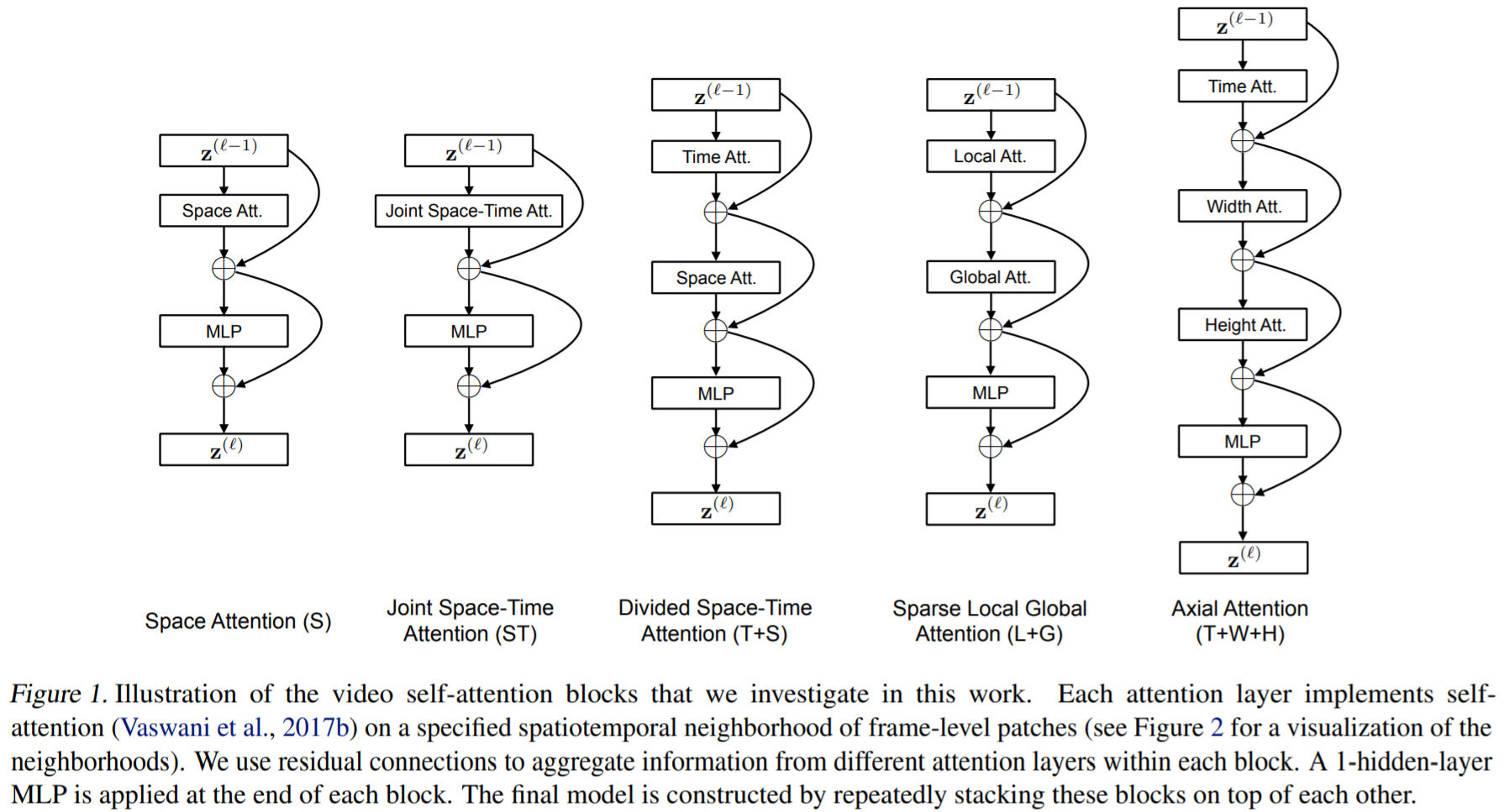
그래서 본 논문에서는 보다 효과적인 **Divided Space-Time Attention (denoted with T+S)**를 제안하였습니다. 이 방법은 tempolar-attenntion을 먼저 적용하고, spatial-attention을 나중에 적용하는 architecture입니다. 실험에서 사용한 다양한 attention layer 조합은 아래 그림에서 볼수 있습니다.
이해를 위해서 이를 visualization하면, 아래와 같습니다.
각 architecture를 간단히 정리하면,
- Joint Space-Time Attention(ST)
- spatiotempolar attention을 적용
- computation per patch: NxF+1
- Divided Space-Time Attention(T+S)
- tempolar-attention(F) 후, spatial-attention(N)를 수행
- computation per patch: N+F+1
- Sparse Local Global Attention (L+G)
- H/2 x W/2에 대한 spatiotempolar attention(local attention)(FxH/2xW/2) 후, 2 stride로 spatiotempolar attention(global aattention)(FxH/2xW/2)을 진행
- computation per patch: FxN/2+1
- Axial Attention (T+W+H)
- tempolar-attention(F) 진행후, W축 attention(W)와 H축 attention(H)를 진행
- computation per patch: T+W+H
4. Experiment
- Dataset(Acition recognition)
- Kinetics-400 (Carreira & Zisserman, 2017)
- Kinetics-600 (Carreira et al., 2018)
- Something-SomethingV2 (Goyal et al., 2017)
- Diving-48 (Li et al., 2018)
- Base architecture
- “Base” ViT model architecture (Dosovitskiy et al., 2020) pretrained on ImageNet (Russakovsky et al., 2014)
- Train
- clip size(FxHxW): 8×224×224
- frame sample rate: 1/16
- patch size: 16 × 16
- Inference
- sample a single temporal clip in the middle of the video
- use 3 spatial crops (top-left, center, bottom-right)
- final prediction: averaging the softmax scores of these 3 predictions.
4.1 Analysis of Self-Attention Schemes
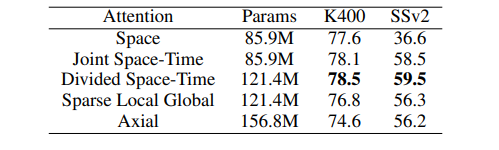
각 self-attention scheme들간 model size, 연상량, 성능을 비교하였습니다.
- Dataset별 중요 정보의 차이
- K400의 경우, spatial information이 중요함
- SSv2의 경우, 상대적으로 temporal information이 중요함.
- divided space-time attention의 결과가 joint space-time attention에 비해 더 좋음.
- space-time attention의 learning-capacity(parameter 수)가 더 큼
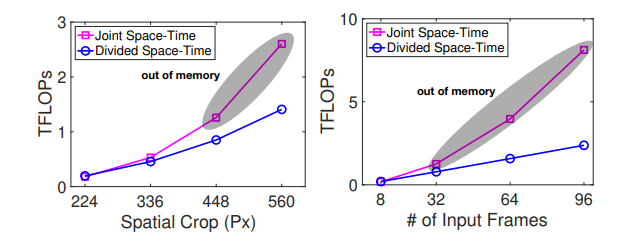
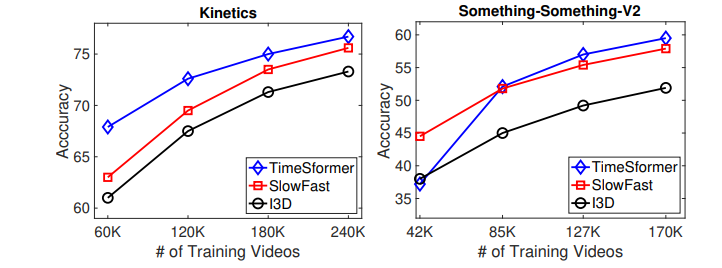
divided space-time attention과 joint space-time attention의 scalability를 비교했습니다. higher spatial resolution (left) 과 longer (right) videos에서 모두 divided space-time attention이 더 큰 size에도 불구하고 더 좋은 scalability를 보여줍니다. 이후 실험부터, divided space-time attention을 default로 사용합니다.
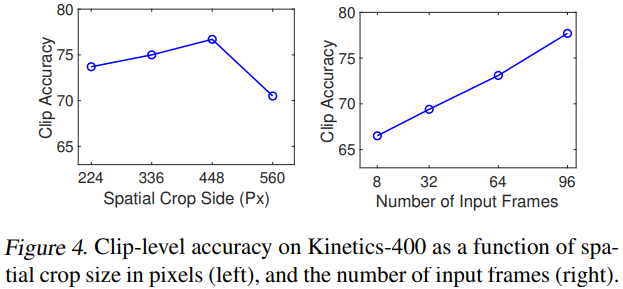
4.2 Varying the Number of Tokens in Space and Time
입력 token 수에 영향을 주는 요소는 spatial resolution을 늘려 N을 증가 시키거나, frame을 늘려 F를 증가시키는 것입니다. 위 그림과 같이, spatial resolution(up to certain point)과 frame 증가는 모두 performance의 증가를 보였습니다. 특히 frame의 경우, memory 제한으로 실험이 불가능한 96 frame까지 계속된 성능 향상을 보였습니다. 보통 CNN기반 video task에서 8~32 frames을 사용하는걸 고려하면, 96 frames은 매우 긴 시간입니다.
4.3 The Importance of Pretraining and Dataset Scale
Transformer를 사용한 model의 경우, 매우 큰 dataset들로 train을 시켜야 결과가 좋게 나오는 경향이 있습니다. 이를 실험하기 위해, 우선 TimeSformer를 scratch부터 학습을 시키려고 하였지만, 잘 되지 않았다고 되어 있습니다. 그래서, 이후 실험에서는 모두 ImageNet으로 pre-training된 model을 사용하였습니다. 학습에 사용한 dataset의 크기별, 25%/50%/75%/100%, 성능은 아래 그림과 같습니다.
K400의 경우, 모든 subset에서 TimeSformer가 가장 좋은 성능을 보였습니다. SSv5의 경우, 75%, 100%에서만 가장 좋은 성능을 보였습니다. 이러한 차이는, SSv5가 K400에 비해, 더 복잡한 tempolar pattern들이 있기 때문이라고 분석하였습니다.
4.4 Comparison to the State-of-the-Art
3가지 type의 TimeSformer와 기존 State-of-the-Art model들과 비교하였습니다.
- TimeSformer
- operating on 8 × 224 × 224 video clips
- TimeSformer-HR
- operating on 16 × 448 × 448 video clips
- TimeSformer-L
- operating on 96 × 224 × 224 video clips with 1/4 sampling
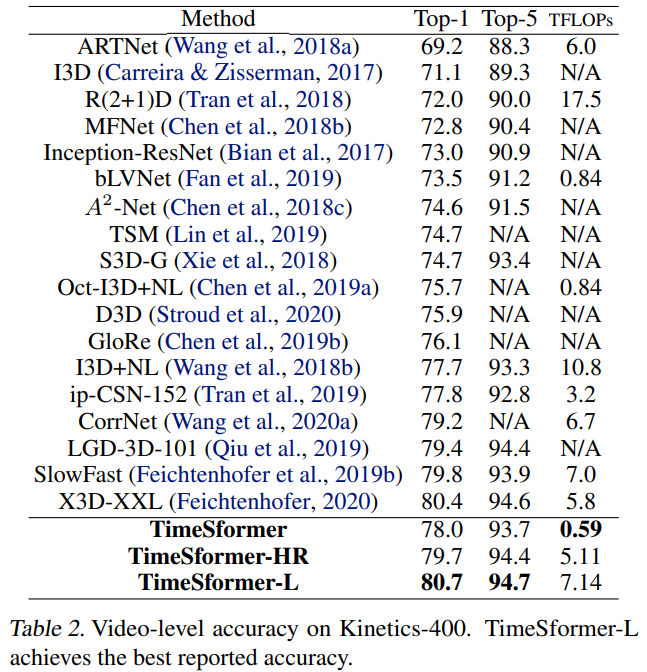
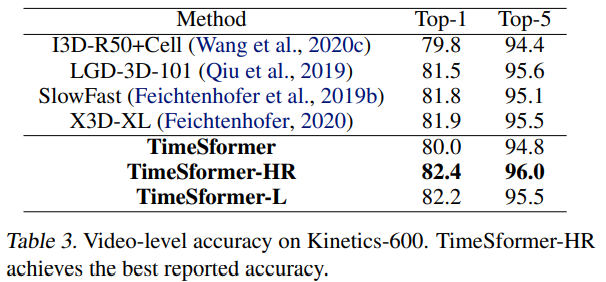
Kinetics-400
위 Table은 K400 dataset에서의 정확도를 기존 model들과 비교하였습니다. Inference시 사용한 input은 아래와 같이 moethod 마다 차이가 있습니다.
- Most previous methods: 10 temporal clips with 3 spatial crops (30 views)
- shorter spatial side를 기준으로 scale 후, left-center-right 3 crops 사용
- TimeSformer: only 3 views (3 views)
- top-left, center, bottom-right 3 crops 사용
이러한 views의 차이로 TimeSformer가 가장 적은 inference cost로 비교할만한 정확도를 얻었을 수 있었습니다. 또한 TimeSformer-L은 가장 좋은 정확도를 보였습니다.
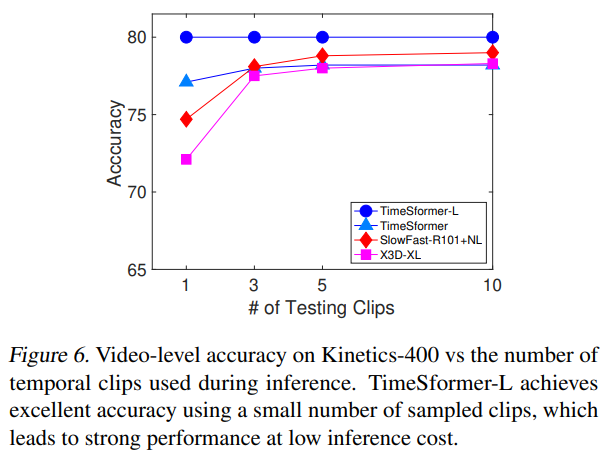
inference에 사용하는 clips수가 성능에 미치는 영향은 위 그림을 통해서 볼수 있습니다. TimeSformer-L의 경우, 1 clip이 전후 96frames(12sec in Kinetics video)를 cover하기 때문에, 1 clip에서도 충분히 좋은 성능을 보입니다. 한가지 아쉬운 부분은, 1 clip 처리를 위한 cost가 method마다 다르기 때문에, cost도 같이 보여주면 더 좋겠다는 생각이 듭니다.
추가하여, transfomer를 이용한 TimeSformer의 경우, CNN기반 model 대비 training 속도에서도 장점을 보입니다. 대략적으로 CNN에 비해, x3 배정도 training 속도가 빠릅니다.
- 8×8 R50 on K400 takes 54.3 hours on 64 GPUs
- I3D R50 under similar settings takes 45 hours using 32 GPUs
- TimeSformer can be trained in 14.3 hours using 32 GPUs
Kinetics-600
k600 dataset에서도 k400과 비슷하게 좋은 결과를 보입니다. 한가지 특이한 점은, k400과 다르게 TimeSformer-HR이 가장 좋은 성능을 보입니다.
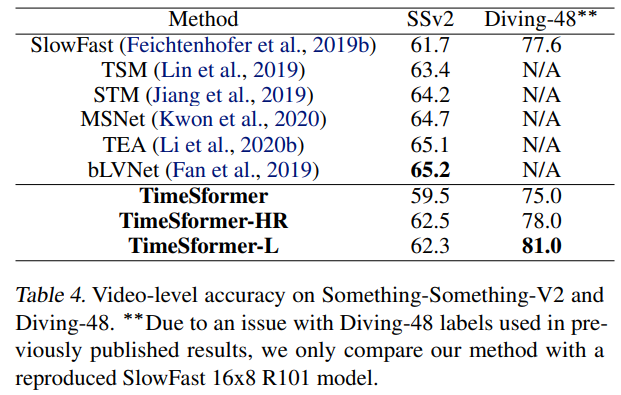
Something-Something-V2 & Diving-48
temporally-heavy datasets인 SSv2와 Diving-48에서의 결과입니다.
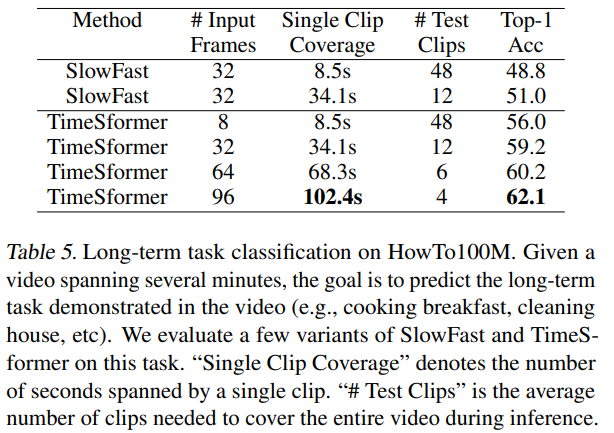
4.5. Long-Term Video Modeling
조금 더 긴 term의 video에 대한 성능 비교를 위해서, HowTo100M dataset의 sub-set을 random하게 만들어 사용하였습니다. HowTo100M은 평균 7분정도의 길이를 가지고 있습니다.
table에서 SlowFast는 2 경우 모두 32 frames을 input으로 사용하였습니다. 다른 점은, sampling 주기로, 각각 1/8(1초에 4개 정도) 그리고 1/32(1초에 1개 정도)를 사용하였습니다. TimeSformer의 경우, sampling 주기는 모두 1/32로 동일하게 하고, 대신 input frame을 가변하였습니다. clips수는 video full로 cover할수 있도록 뽑았으며, 최종 classification은 각 clip 결과를 평균하였습니다.
같은 single-clip coverage model을 비교시 7~8% 정도 좋은 성능을 보였습니다. 96 frames을 inpput으로 받은 TimeSformer이 가장 좋은 성능을 보였습니다.
이를 통해, TimeSformer이 long-range video modeling에 좋은 구조이며, video feature 추출을 위한 model로 사용하기 좋다고 결론 짓습니다.
5. Conclusion
이전까지 video modeling 방법들, convolution-based video networks,과 다른 self-attention에 기반을 둔 TimeSformer를 제안하였습니다. TimeSformer의 장점은 simple한 구조와 low inference cost 그리고 long-term video modeling에 강한다는 것입니다.
하지만 상대적으로 temporally-heavy dataset에서는 좋은 성능을 보여주지 못했습니다. 개인적으로 tempolar domain을 많이 희생해서, computation cost를 감소 시켰다고 생각합니다.