dj-woo.github.io
Transformer
개인 study를 위한 자료입니다.
그러다보니 내용에 잘못된 점이 있습니다.
1.Introduction & 2.Background
기존 방법들에 대한 언급과 장단점을 기술하였습니다. 실제 transformer 구현에 대한 설명은 3절부터 시작됩니다.
3. Model Architecture
- transformer의 model architecture는 아래와 같습니다.
in/out 관계
- x = an input sequence of symbol representations
- z = a sequence of continuous representations
- y = an output sequence
- z = encoder(x)
- y = decoder(z)
3.1 Encoder and Decoder Stacks
- Encoder: 2개의 sub-layer로 구성됨.
- multi-head (self) attention
- (fully connected) feed-forward network
-
Decoder: 3개의 sub-layer로 구성됨.
- 2개의 sub-layer는 encoder와 같음.
- masked multi-head attention: multi-head attention에 decoder의 특성을 반영하기 위해 mask를 추가하였습니다.
predictions for position i can depend only on the known outputs at positions less than i.
각 sub-layer에는 residual connection이 있고, 뒤에 normalization layer가 붙어 있습니다.
따라서, 각 sub-layer의 output은 LayerNorm(x + Sublayer(x)) 입니다. 이 절에서 논문에 전의된 변수는 아래와 같습니다.
- Encoder: stack N = 6, d_model = 512
- Decoder: stack N = 6
3.2 In Attention
3.2.1 Scaled Dot-Product Attention
- Q, K =
$d_k$ - V =
$d_v$=$d_{model}$
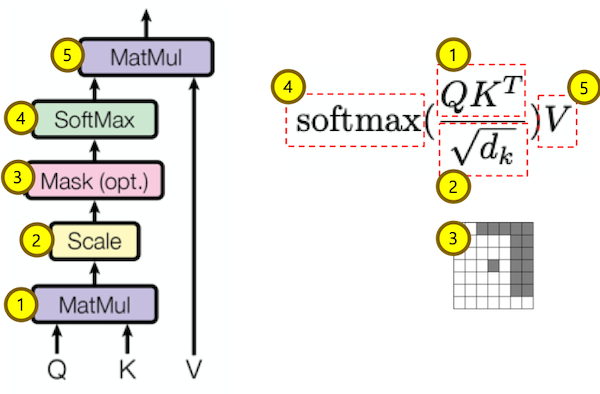
Scaled Dot-Product attention layer는 위에 그림처럼, $QK^T$에 softmax를 취하여 weight을 계산합니다. 그리고, 이 값을 Value와 곱하는 layer입니다. 전체 식은 아래와 같습니다.
$$ Attention(Q,K,V) = {softmax(\frac{QK^T}{\sqrt{d_k}})V} $$
여기서 $\sqrt{d_k}$로 나누는 이유는 $\sqrt{d_k}$의 값이 거질수로, dot-product의 결과값이 softmax가 잘 동작하지 않는 regions으로 가기 때문입니다.
paper: To illustrate why the dot products get large, assume that the components of q and k are independent random variables with mean 0 and variance 1. Then their dot product,
${qk} = {\sum_{i=1}^{d_k}q_iK_i}$, has mean 0 and variance$d_k$.
3.2.2 Multi-head Attention
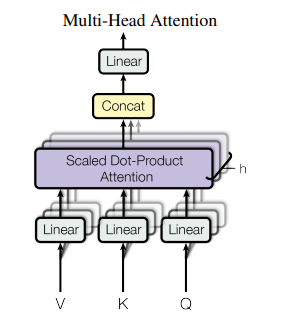
$d_{model}$의 K,Q,V에 하나의 attention을 적용하는 것보다, 각각을 h 번 서로 다른 $d_{k}$,$d_{q}$,$d_{v}$로 linear project 하여, 각각에 attention function을 병렬적으로 수행하는게 더 좋다는 것을 발견했다고 논문에 나와 있습니다. h개의 $d_{v}$을 concat하고 한번 더 project 하면 input과 동일한 값을 얻을 수 있습니다. 식으로 나타내면 아래와 같습니다. $$ MultiHead(Q,K,V) = { Concat(head_1,....,head_h)W^O}\\ where\ {head_i} = Attention(QW_i^Q, KW_i^K, VW_i^K)$$
$W_i^Q, W_i^K, W_i^K$는 각각 $d_{model}$의 input을 $d_q, d_k, d_v$로 linear project 시켜줍니다. 논문에서는 사용한 값은 아래와 같습니다. h개의 head를 사용하지만, dimension을 1/h로 줄였기 때문에, total computational cost는 single head를 사용할때와 유사합니다.
$ h = 8, d_k=d_q=d_v=d_{model}/h=64$
paper: we found it beneficial to linearly project the queries, keys and values h times with different, learned linear projections to dk, dk and dv dimensions, respectively.
paper: Due to the reduced dimension of each head, the total computational cost is similar to that of single-head attention with full dimensionality.
3.2.3 Applications of Attention in our Model
앞에 내용을 정리해서, 적용한 attention model의 특징을 3가지로 설명 합니다.
- “encoder-decoder attention layer”에서 query는 앞단의 decoder layer에서 오고, key와 value는 encoder의 저장된 output입니다. 이렇게 해서, decoder의 모든 position에서 input sequence의 모든 position을 참조 할 수 있습니다. 이때까지, 앞단의 decoder에서 받는 값은 value라고 생각했는데, query 네요..
- encoder는 self-attention layer를 사용합니다. encoder의 각 position을 계산할때는, 모든 position을 참조합니다.
- encoder와 비슷하게, decoder도 self-attention layer가 있습니다. 다른 점은, decoder의 각 position을 계산할때는 해당 position과 그 이전 position까지의 data만 사용할 수 있습니다.
3.3 Position-wise Feed-Forward Networks

$d_{model} = 512$이지만, inner-layer는 4배 많은 $d_{ff}=2048$을 사용합니다.
- size(W1) =
$d_{model}\ \times\ d_{ff} = 512 \times 2048 $ - size(W2) =
$d_{ff}\ \times\ d_{model} = 2048 \times 512 $
3.4 Embeddings and Softmax
input/output 문장($[128\ \times\ 1]$)이 주어지면, 한 단어를 뜻하는 token을 vector($[1\ \times\ $d_{model}]$)로 변환해주는 embedding을 합니다. 논문에서는 미리 학습된 embedding 을 사용했다고 나와있습니다. decoder의 output을 처리하기 위해서도 비슷한 과정이 필요합니다. embedding의 역행렬 개념인 pre-softmax linear transformation을 하고, softmax function을 통해서, decoder output을 next-token의 확률로 변환합니다. input/output을 처리하기 위한 embeding과 pre-softmax linear transformation에는 동일한 weight matrix를 사용했습니다. 그리고 embedding layer에는 $\sqrt{d_{model}}$를 weight에 곱했습니다.(????)
3.5 Positional Encoding
recurrence, convolution을 사용하지 않았기 때문에, sequence의 order를 model이 학습할 수 있도록, position에 대한 값을 추가해야합니다. 이를 위해서, embedding step에 “positional encoding”을 추가했습니다. positional encoding도 embedding과 동일한 dimension $d_{model}$을 가지기 때문에, 2 값을 합이 가능합니다. positional encoding을 위해서 사용한 식은 아래와 같습니다. $$ PE_{(pos,2i)} = sin(pos / 1000^{2i/d_{model}})\\ PE_{(pos,2i+1)} = cos(pos / 1000^{2i/d_{model}}) $$ 이 식을 선택한 이유는, pos값에 상관없이 pos+k와 pos간의 관계가 linear하기 때문에, model이 relative position관계를 학습하기 쉽기 때문입니다.
paper: We chose this function because we hypothesized it would allow the model to easily learn to attend by relative positions, since for any fixed offset k,
$PE_{pos+k}$can be represented as a linear function of$PE_{pos}$.
4 Why Self-Attention
- n = sequence length, d = representation dimension, k = kernel size of convolutions, r = size of the neighborhood in restricted self-attention.
본 논문에서는 self-attention layer를 사용하여 x를 동일한 길이의 sequence vector z에 mapping 하였습니다. self-attention layer를 사용한 이유로 recurrent layer와 convolution layer와 비교하여 아래 3가지를 들었습니다.
- complexity per layer
- sequential operations
- path length between long-range dependencies (Maximum Path Length)
3번 Maximum PaTH Length는 이해하기가 그나마 쉽습니다.
2번은 Convolutional layer가 $O(log_k(n)$가 되야 할것 같은데, $O(1)$인 이유를 잘 모르겠습니다. 1번은 self-attention만 한 단위 계산 복잡도가 $d$이고 recurent와 convolutional은 $d^2$인데, 이 이유를 잘 모르겠습니다.
그외에 side-benefit으로 interpretable models이라는 점을 들었습니다.
5 Training
실제 training 시킨 조건에 대한 설명이 있습니다. 몇몇 부분이 구현과 관련있습니다.
5.3 Optimizer
Adam optimizer를 사용했습니다.
5.4 Regularization
3가지 type(?)의 regularization을 사용했습니다.
- Residual Dropout: 각 sub-layer output 에 사용 (Pdrop = 0.1)
- Residual Dropout: embedding + positional embedding 결과 값에 사용 (Pdrop = 0.1)
- Label Smoothing: 이 방법은 model 이 확실한 결과값을 학습하지 못하게 하지만, BLEU score에 도움이 되었다고 합니다.
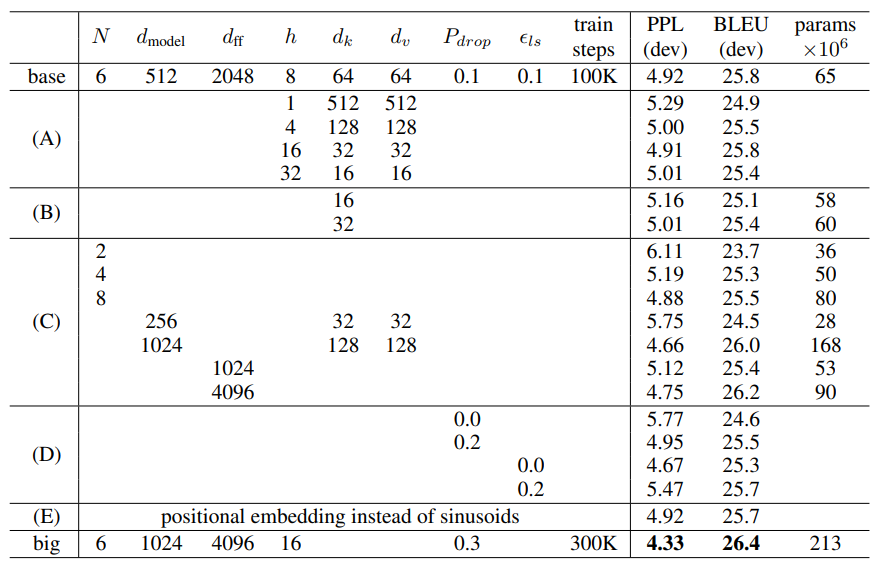
6.2 Model Variations
hyper parameter를 변경하면서 performance를 비교하였습니다. model에서 사용한 hyper parameter가 어떤 것들이 있는지 한눈에 보기 좋습니다.
(A): header 수에 변화를 주었습니다. 너무 많아도 성능이 저하 됩니다.
(B): key dimension 에 작으면 성능이 나빠집니다.
(C): 예상과 같이, “bigger is better” 임을 보여주는 결과 입니다.
(D): drop-out 은 꼭 해야함.
(E): positional encoding 을 미리 학습된 model를 사용한 겱과입니다. 결과는 큰 차이없습니다.